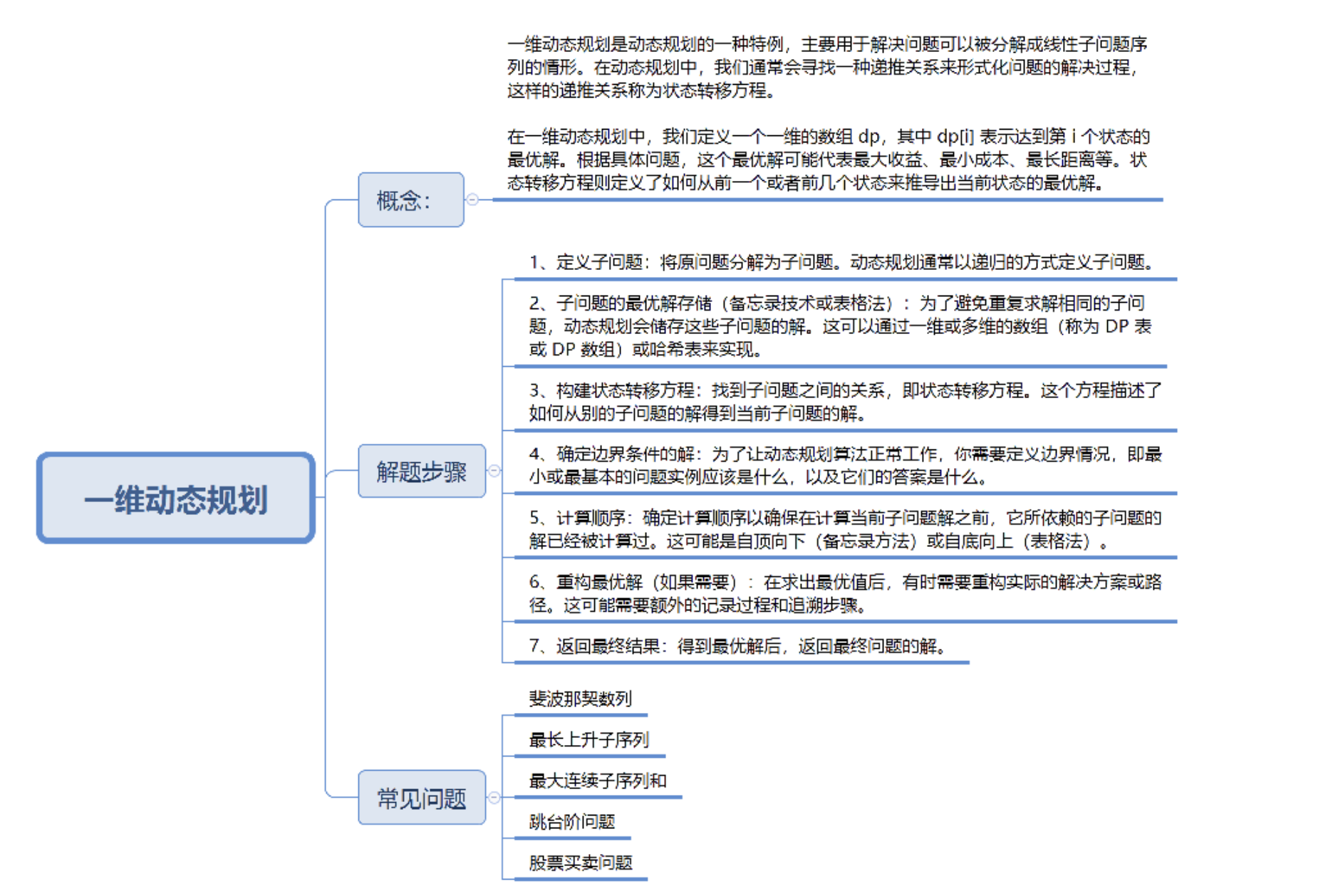
一维动态规划
登录以参加训练计划
什么是动态规划?
想象你要组装一个超大的乐高城堡!如果直接从最顶层开始拼,可能会手忙脚乱。但如果一层一层从下往上搭,每一步都稳稳的,最后就能轻松完成啦!
动态规划就像这样:把大问题拆成小问题,先解决小问题,再用小问题的答案一步步解决大问题!
🐾 一维动态规划是什么?
用一个魔法数组(比如叫 dp)来记录每一步的答案!
就像小兔子跳台阶的题目:
题目:
小兔子要跳上第 5 级台阶,每次能跳 1 级或 2 级。有多少种不同的跳法?
用动态规划解决:
分解问题:
跳到第 5 级台阶的跳法 =
(跳到第 4 级的跳法 + 再跳 1 级)
+
(跳到第 3 级的跳法 + 再跳 2 级)
魔法数组 dp:
dp[0] = 1(站在地面算 1 种方法)dp[1] = 1(跳到第 1 级只有 1 种方法)dp[2] = dp[1] + dp[0] = 2dp[3] = dp[2] + dp[1] = 3- ……
- 一直算到
dp[5] = 8!
规律公式:
dp[n] = dp[n-1] + dp[n-2](因为最后一步可能是跳 1 级或 2 级)
✨ 一维动态规划的秘诀
-
拆解问题: 把大问题变成更小的同类问题(比如跳 5 级→跳 4 级 + 跳 3 级)。
-
记住答案: 用数组
dp记录每个小问题的答案,避免重复计算。 -
逐步解决: 像搭积木一样,从最底层开始,一步步算到目标!
🌰 举个栗子:存钱罐问题
你有 1元、2元硬币,存满 4元有多少种组合?
动态规划解法:
- 魔法数组
dp:dp[i]表示存满i元的方法数。 - 初始值:
dp[0] = 1(0元只有“不放硬币”1种方法)
- 递推公式:
- 如果加上 1元硬币:
dp[i] += dp[i-1] - 如果加上 2元硬币:
dp[i] += dp[i-2]
- 如果加上 1元硬币:
- 结果:
dp[4] = 5(1+1+1+1, 1+1+2, 1+2+1, 2+1+1, 2+2)
🌈 总结
一维动态规划就像魔法笔记本:
- 把大问题拆成小问题,
- 把每个小问题的答案记在本子上,
- 用已有的答案一步步算出大问题的解!
下次遇到难题时,试试这个方法吧!😊
章节 1. 新手
开放
| 题目 | 尝试 | AC | 难度 |
|---|---|---|---|
| P474 【例86.1】 上台阶 | 23 | 5 | 8 |
| P513 最长上升子序列 | 22 | 8 | 7 |
| T1289 练4 拦截导弹 | 38 | 9 | 7 |
| T1283 登山 | 33 | 5 | 8 |
| P475 【例86.2】 01背包问题 | 43 | 8 | 8 |
| T1206 放苹果 | 25 | 9 | 7 |
| P476 【例86.3】 完全背包问题 | 47 | 7 | 8 |
章节 2. 师傅
开放
| 题目 | 尝试 | AC | 难度 |
|---|---|---|---|
| P477 【例86.4】 混合背包 | 12 | 3 | 9 |
| T1265 【例9.9】最长公共子序列 | 13 | 3 | 9 |
| P1135 「一本通 5.5 例 1」滑动窗口 | 5 | 3 | 10 |
| P1136 「一本通 5.5 例 2」最大连续和 | 26 | 1 | 10 |
| P1137 「一本通 5.5 例 3」修剪草坪 | 3 | 1 | 10 |
| P1138 「一本通 5.5 例 4」旅行问题 | 1 | 1 | 10 |
| P1139 「一本通 5.5 例 5」Banknotes | 1 | 0 | 10 |
| P1140 「一本通 5.5 练习 1」烽火传递 | 4 | 0 | 10 |
| P1141 「一本通 5.5 练习 2」绿色通道 | 1 | 0 | 10 |
| P1142 「一本通 5.5 练习 3」理想的正方形 | 2 | 1 | 10 |
| P1143 「一本通 5.5 练习 4」股票交易 | 7 | 1 | 10 |
章节 3. 大神
开放
| 题目 | 尝试 | AC | 难度 |
|---|---|---|---|
| T1269 【例9.13】庆功会 | 8 | 1 | 10 |
| T1270 【例9.14】混合背包 | 5 | 3 | 10 |
| T1271 【例9.15】潜水员 | 1 | 1 | 10 |
| T1272 【例9.16】分组背包 | 0 | 0 | (无) |
| T1273 【例9.17】货币系统 | 1 | 1 | 10 |
| T1290 采药 | 18 | 6 | 8 |
| T1291 数字组合 | 0 | 0 | (无) |
| T1292 宠物小精灵之收服 | 0 | 0 | (无) |
| T1293 买书 | 0 | 0 | (无) |
| T1294 Charm Bracelet | 0 | 0 | (无) |
| T1295 装箱问题 | 0 | 0 | (无) |
| T1296 开餐馆 | 0 | 0 | (无) |
